5363. Drying
Washing clothes in winter is no easy task, and drying them is
even more challenging. But Jane is a clever girl and isn’t afraid of routine
chores. To speed up the drying process, she decided to use a radiator. However,
the radiator is small and can dry only one item at a time.
Jane wants to dry the laundry as quickly as possible. She’s
asking you to write a program that determines the minimum amount of time needed
to dry the entire set of clothes.
Jane has just washed n items. During the wash, each
item absorbed aᵢ units of water. Every minute, the amount of water
in each item decreases by one unit (as long as the item is not yet dry). Once
the amount of water reaches zero, the item is considered dry and can be packed.
Additionally, each minute, Jane can choose one item and place
it on the radiator. The radiator is hot enough that an item placed on it loses k
units of water per minute (but no more than the amount of water it contains: if
an item has less than k units of water, it simply dries completely in
that minute).
Your task is to determine the minimum amount of time needed
to dry all the clothes with optimal use of the radiator. Drying is considered
complete when all items are fully dry.
Input. The first line contains a single integer n (1 ≤ n
≤ 105) – the number of items.
The second line contains n integers ai (1 ≤ ai ≤ 109), where ai is the amount of water in the i-th item after
washing.
The third line contains a single integer k (1 ≤ k ≤ 109) – the evaporation rate of
water from an item placed on the radiator (in units of water per minute).
Output. Print a single integer – the
minimum number of minutes required to completely dry all items.
|
Sample
input |
Sample
output |
|
3 2 3 9 5 |
3 |
SOLUTION
binary search
Algorithm analysis
Let max
be the largest value among all ai.
Obviously, after max minutes, all the laundry will dry naturally, even
without using the radiator.
Let the answer
be a value m. This means that all items containing at most m
units of water will have enough time to dry naturally. Any item that contains
more than m units of water will require additional drying on the
radiator.
We assume that
each item loses 1 unit of water per minute, regardless of whether it is on the
radiator or not. However, if an item is placed on the radiator, it loses an
additional k – 1 units of water per
minute, meaning it loses k units per minute in total.
If m
minutes are enough to dry all the items, then each item with ai > m must be additionally dried using the radiator. The amount of
water that won't evaporate naturally is ai
– m. Since the radiator removes k – 1 extra units of
water per minute, this item will require
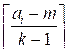
minutes of
radiator time.
The total number of
minutes 
the radiator is used must
not exceed m, since only one item can be dried per minute. The summation
is taken over all indices i for which ai > m.
Thus, the check is
performed as follows: if, for a given value of m, the total required
radiator time does not exceed m, then this value of m is
considered valid. The smallest valid value of m can be found using
binary search.
Example
Initially, there
are three items with water amounts: (2, 3, 9).
In the first
minute, place the third item on the radiator. The state becomes: (1, 2, 4).
In the second
minute, again place the third item on the radiator. The state becomes: (0, 1,
0).
In the third
minute, the second item dries naturally. The final state is: (0, 0, 0).
Let’s consider the value m = 2. In this case, all items
containing no more than 2 units of water will dry naturally.
The remaining items will
require drying using the radiator.
The second item contains 3
units of water, so the radiator needs to remove 3 – 2 = 1 unit.
The third item contains 9
units of water, so the radiator needs to remove 9 – 2 = 7 units.
This will take 
+ 
= 3 minutes. This exceeds m = 2, so two minutes are not enough.
Algorithm implementation
Declare the array.
#define MAX 100001
int a[MAX];
Read the input data.
scanf("%d",&n);
for(i = 0; i < n; i++) scanf("%d",&a[i]);
scanf("%d",&k);
In r minutes, all the laundry will definitely dry, even without
using the radiator.
l = 0; r =
*max_element(a,a+n);
If k ≤ 1, then drying with the
radiator is equivalent to natural drying, and the radiator provides no
advantage.
if (k <= 1)
{
printf("%d\n",r);
return 0;
}
The minimum required number of minutes m can be
found using binary search on the interval [l;
r].
while
(r - l > 1)
{
m = (r + l) / 2;
The variable dry accumulates the total number of
minutes during which the radiator needs to be used. All the laundry must be
dried within m minutes.
dry = 0;
for (i = 0; i < n; i++)
{
if (a[i]
> m)
dry += (a[i] - m + k - 2) / (k - 1);
if (dry
> m) break;
}
if (dry >
m) l = m; else r = m;
}
Print the answer.
printf("%d\n",r);